1. 버블 정렬
: 양옆에 위치한 두 값을 비교하면서 크기 순으로 정렬 -> 배열의 뒤에서부터 정렬됨
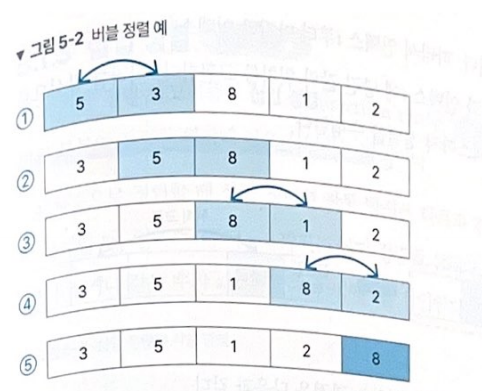
배열의 n번째 요소를 정렬하기 위해 n(n-1)/2만큼 연산을 수행하며, O(n^2)의 시간 복잡도 소요됨. 정렬 수행이 비교적 느리지만 별도의 메모리 공간이 필요하지 않음
2. 선택 정렬
: 배열을 순회하면서 배열의 앞에서부터 차례대로 각 인덱스에 들어갈 값을 선택해 위치시킴

배열의 n번째 요소를 정렬하기 위해 n(n-1)/2만큼 연산을 수행하며, O(n^2)의 시간 복잡도 소요됨. 정렬 수행이 비교적 느리지만 별도의 메모리 공간이 필요하지 않음. 하지만 구현이 비교적 간단함.
3. 삽입 정렬
: 배열을 앞에서부터 순회하면서 정렬된 부분의 적절한 위치에 값을 삽입하는 방식

배열의 n번째 요소를 정렬하기 위해 n(n-1)/2만큼 연산을 수행하며, O(n^2)의 시간 복잡도 소요됨.
4. 합병 정렬
: 정렬하는 배열을 크기가 0 또는 1이 될 때까지 절반씩 분할하고, 분할된 각각의 배열은 다시 하나의 배열로 합치면서 정렬을 수행

합병 정렬의 시간 복잡도는 O(n log n)으로 수행 시간 면에서 효율적임
5. 퀵 정렬
: pivot 이라는 특정 값을 선택해 피봇보다 작은 값으로 구성된 배열과 피봇보다 큰 값으로 구성된 배열로 분열해 정렬하는 방식 -> 분할 배열의 크기가 1 이하가 될 때까지 반복해서 수행함
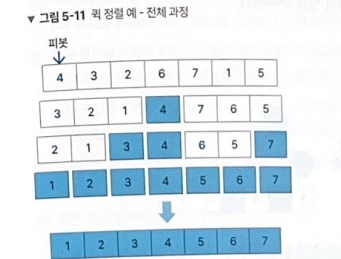
평균적인 시간 복잡도는 O(n log n)임 -> 이를 위해서 배열을 균등하게 분할할 수 있어야 함. 피봇 선택이 중요!
6. 힙 정렬
: 배열을 힙으로 만드는 과정을 통해 최대 힙이나 최소 힙 자료구조를 이용해 정렬을 수행 -> 시간 복잡도는 O(n log n)

7. 기수 정렬
: bucket이라는 큐를 생성해 낮은 자릿수부터 정렬을 수행
데이터 개수를 n, 최대 자릿수를 d라고 할 때 시간 복잡도는 O(dn)임
8. 계수 정렬
: 데이터의 개수를 세서 정렬하는 방식
데이터의 개수를 n, 데이터의 최댓값을 k라고 할 때 시간 복잡도는 O(n+k)임
'공부 기록 > CS' 카테고리의 다른 글
| 5.3 최단 거리 알고리즘 (0) | 2024.08.14 |
|---|---|
| 5.2 최소 신장 알고리즘 (0) | 2024.08.13 |
| 4단원 요약정리 (0) | 2024.08.09 |
| 4.3 비선형 자료구조 (3) (0) | 2024.08.08 |
| 4.3 비선형 자료구조 (2) (0) | 2024.08.07 |
